Abbildungen01 >>

Geometrische Abbildungen und Matrizen

Wir haben Vektoren und Matrizen in vielen verschiedenen Zusammenhängen kennengelernt. Sie spielten eine Rolle bei der Entwicklung von Käuferzahlen von Produkten, beim Lösen von linearen Gleichungssystemen, bei Wirtschafts- und Finanzprozessen. Man kann Vektoren nun auch als Punkte in der Ebene oder im Raum auffassen: Die Koeffizienten des Vektors sind einfach die Koordinaten eines Punktes.

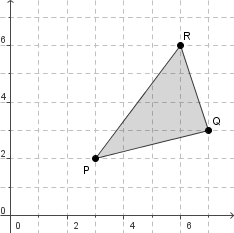
Die Vektoren

\vec{p}=\left(3\atop 2\right),\quad\vec{q}=\left(7\atop 3\right),\quad \vec{r}=\left(6\atop 6\right)

stehen für die Punkte

P(3|2),\quad Q(7|3),\quad R(6|6)

Wir wollen nun untersuchen, was mit diesen Vektoren bei der Multiplikation mit verschiedenen Matrizen passiert.

Für die Matrix

A=\left(\begin{array}{cc} -0{,}6&0{,}8\\0{,}8&0{,}6\end{array}\right)

erhält man die Bildpunkte

{$ \vec{p}'=A\cdot\vec{p}=\left(-0{,}2\atop 3{,}6\right)\qquad \vec{q}'=A\cdot\vec{q}=\left(-1{,}8\atop 7{,}4\right)\qquad \vec{r}'=A\cdot\vec{r}=\left(1{,}2\atop 8{,}4\right) $}

Das Bilddreieck ergibt sich aus einer Spiegelung an der Ursprungsgeraden s.

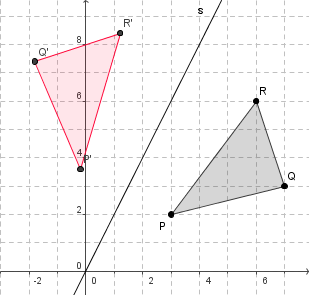
Untersuche mit Geogebra, wie die drei Punkte durch weitere Matrizen abgebildet werden:

{$ B=\frac{1}{13}\left(\begin{array}{cc} 12&-5\\-5&-12\end{array}\right)\qquad C=\frac{1}{2}\left(\begin{array}{cc} \sqrt{3}&-1\\1&\sqrt{3}\end{array}\right)\qquad D=\frac{1}{2}\left(\begin{array}{cc} -\sqrt{2}&-\sqrt{2}\\\sqrt{2}&-\sqrt{2}\end{array}\right) $}

Geogebra-Datei

Abbildungen01 >>