Affine Abbildungen
Definition: Eine Abbildung $$ A:\vec{x}\mapsto\vec{x}'=M\cdot\vec{x}+\vec{v} $$ mit einer Abbildungsmatrix M und einem Verschiebungsvektor \vec{v} heißt affine Abbildung.
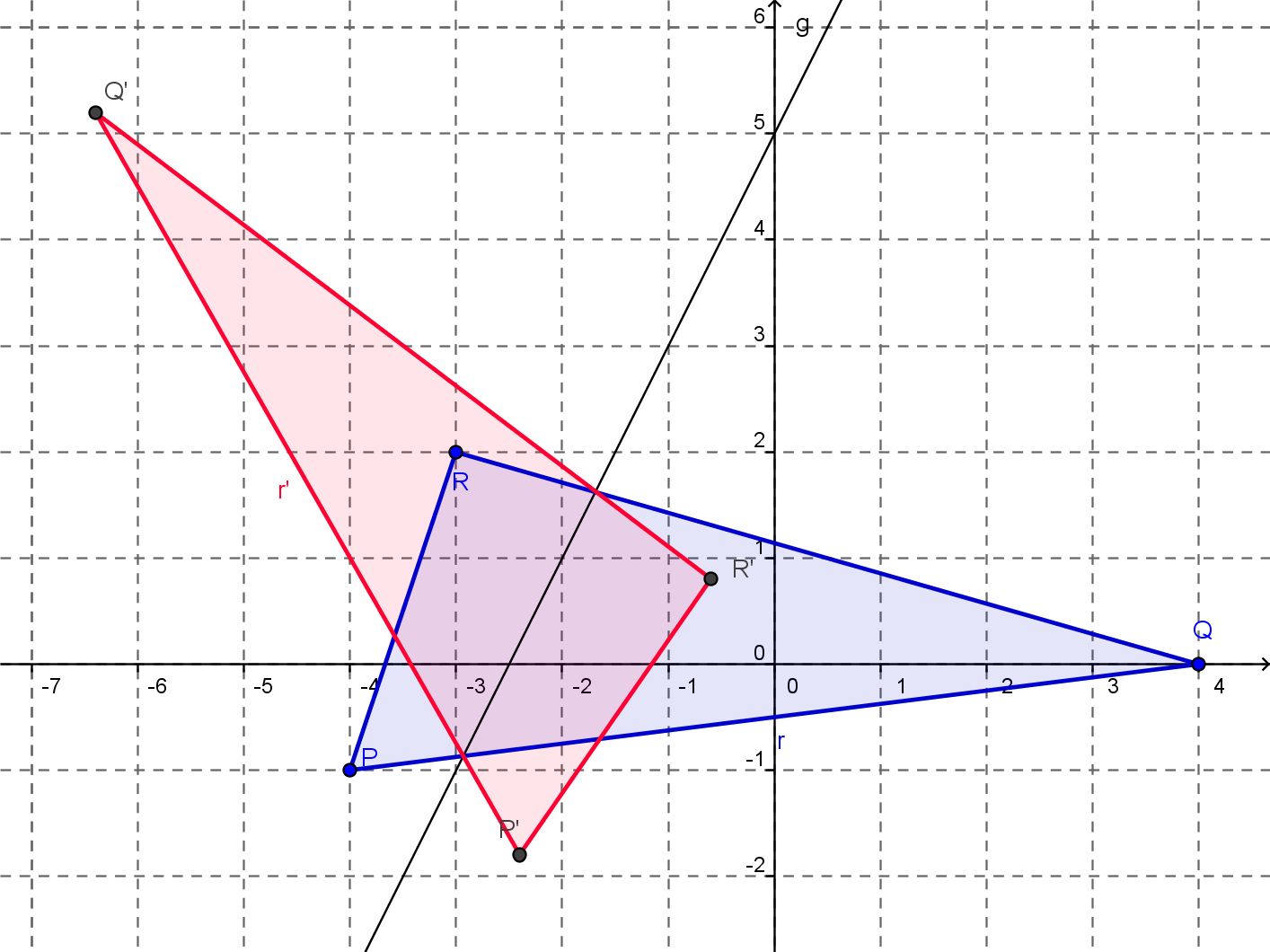
Beispiel 1: Die Abbildung $$ \vec{x}\mapsto\left(\begin{array}{cc} -\frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&\frac{3}{5}\end{array}\right)\cdot\vec{x}+\left(-4\atop 2\right) $$ bildet die Punkte \vec{p},\quad\vec{q} und \vec{r} wie dargestellt ab. Es handelt sich um eine Spiegelung an der Geraden g mit der Steigung 2 durch den Punkt \left(0\atop 5\right).
Beispiel 2: Drehung um ein beliebiges Zentrum
Um die Abbildungsvorschrift einer Drehung um den Winkel \alpha um das Drehzentrum \vec{z} zu erhalten, verschiebt man zuerst so, dass das Drehzentrum im Ursprung liegt, dreht dann mit der passenden Drehmatrix D und schiebt wieder zurück: $$ \vec{x}\mapsto \vec{x}-\vec{z} \mapsto D\cdot(\vec{x}-\vec{z})\mapsto D\cdot(\vec{x}-\vec{z})+\vec{z} = D\cdot\vec{x}+\underbrace{\vec{z}-D\cdot\vec{z}}_{=\vec{v}}$$
Für eine Drehung um 270° um den Punkt Z(3|1) erhält man die Drehmatrix $$ D = \left(\begin{array}{cc} \cos(270°)&-\sin(270°)\\\sin(270°)&cos(270°)\end{array}\right) = \left(\begin{array}{cc} 0&1\\-1&0\end{array}\right) $$ und den Verschiebungsvektor $$\vec{v}=\vec{z}-D\cdot\vec{z}=\left(3\atop 1\right)-\left(\begin{array}{cc} 0&1\\-1&0\end{array}\right)\cdot\left(3\atop 1\right)=\left(2\atop 4\right) $$
Insgesamt ergibt sich als Abbildungsvorschrift $$ A:\vec{x}\mapsto\left(\begin{array}{cc} 0&1\\-1&0\end{array}\right)\cdot\vec{x}+\left(2\atop 4\right) $$ Geogebra-Datei zu Drehungen
Beispiel 3: Spiegelungen an beliebigen Geraden
Die Vorgehensweise, um die Abbildungsvorschrift einer Spiegelung an einer beliebigen Geraden zu erhalten, ist analog zu den Drehungen. Man führt zuerst eine Verschiebung durch, die die Gerade zu einer Ursprungsgeraden macht. Dann wendet man die passende Spiegelmatrix S an und verschiebt zurück. Für die Verschiebung kann jeder Punkt \vec{p} der Geraden verwendet werden. $$ \vec{x}\mapsto \vec{x}-\vec{p} \mapsto S\cdot(\vec{x}-\vec{p})\mapsto S\cdot(\vec{x}-\vec{p})+\vec{p} = S\cdot\vec{x}+\underbrace{\vec{p}-S\cdot\vec{p}}_{=\vec{v}}$$
Für eine Spiegelung an der Geraden durch die Punkte P(-2|-1) und Q(3|5) ergibt sich als Steigung m=2 und damit für die Spiegelmatrix $$ S= \frac{1}{1+m^2}\left(\begin{array}{cc} 1-m^2&2m\\2m&m^2-1\end{array}\right) = \left(\begin{array}{cc} -\frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&\frac{3}{5}\end{array}\right) $$
Für den Verschiebungsvektor ergibt sich $$\vec{v}=\vec{p}-S\cdot\vec{p}=\left(-2\atop -1\right)-\left(\begin{array}{cc} -\frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&\frac{3}{5}\end{array}\right)\cdot\left(-2\atop -1\right)=\left(-\frac{12}{5}\atop \frac{6}{5}\right) $$
Insgesamt ergibt sich als Abbildungsvorschrift $$ A:\vec{x}\mapsto\left(\begin{array}{cc} -\frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&\frac{3}{5}\end{array}\right)\cdot\vec{x}+\left(-\frac{12}{5}\atop \frac{6}{5}\right) $$ Geogebra-Datei zu Spiegelungen